Come on and look inside my head

1. AVL tree란?
AVL tree를 설명하기에 앞서, BST(이진탐색트리)에 대해 알고 있어야 하는데,이는 이전에 내가 작성 했던 글을 참고하면 BST에 대해 간단히 알수 있다.

이 블로그의 이전글 링크 :
이진탐색트리(BST) +(LeetCode 98, 99, 700, 701 풀이) - https://freakingeniousshawn.tistory.com/m/4

BST(이진탐색트리)는 큰 문제점이 있다. 바로 트리가 치우친 모양,바로 한쪽으로 노드가 쏠린 형태가 될 수가 있다. 한 쪽으로 지나치게 치우친 트리는 가장 효율적인 탐색 트리를 추구하는 자료구조의 궁극적 목표와는 먼, 매우 비효율적인 형태이다. 이를 방지하기 위해서는 균형잡힌 모양의 트리가 가장 이상적인데, 이러한 트리를 우리는 Balanced binary tree라고 한다.

Balanced binary tree의 구조를 가지기 위해서 쓰이는 유용한 자료구조가 바로 AVL tree다.

AVL tree는 몇가지 특징이 있는데, 아래와 같다.

1. 이진 탐색 트리의 속성을 가진다.
2. 왼쪽, 오른쪽 서브 트리의 높이 차이가 최대 1이다.
3. 높이 차이가 1보다 커지면 회전(rotation)을 통해 균형을 맞춰 높이 차이를 줄인다.
4. 삽입, 검색, 삭제의 시간 복잡도가 O(log n)이다.

군형이 무너진 트리는 크게 LL,RR,LR,RL의 경우로,
LL(left left)일때는 우회전 적용, RR(right right)일때는 좌회전 적용, LR(left right)일때는 LL의 형태로 만들고 LL해법으로 풀고 RL(right left)일때는 LR과 같은 메커니즘이지만 반대방향으로 해결하면 된다.

AVL Tree를 더 전문적으로 알아보고 싶다면 아래 링크들을 참고하자.
https://www.geeksforgeeks.org/avl-tree-set-1-insertion/

https://www.geeksforgeeks.org/avl-tree-set-2-deletion/

2. AVL tree 코딩
앞서 AVL tree에 대해 열심히 설명했으니 직접 프로그래밍 해보자.

Rank 구현

AVL tree 구현

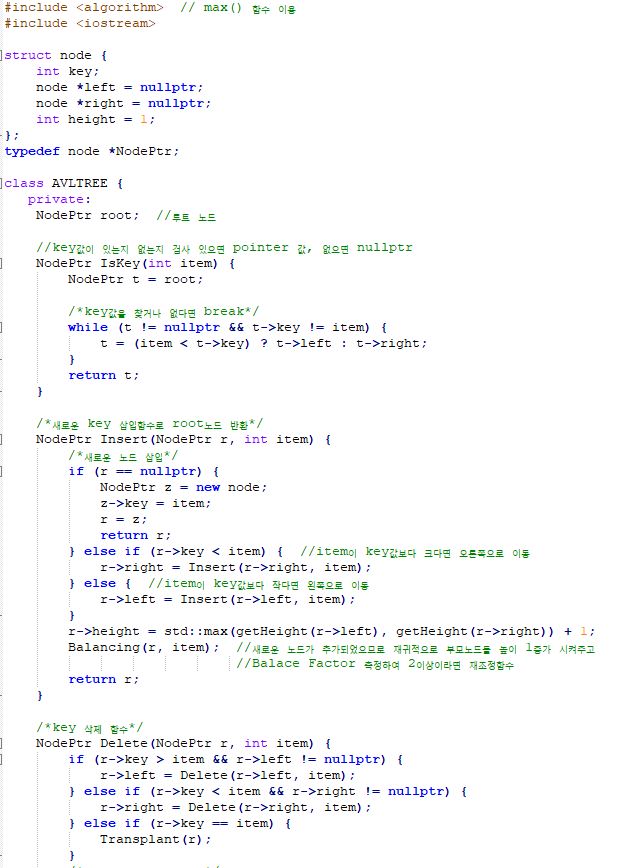
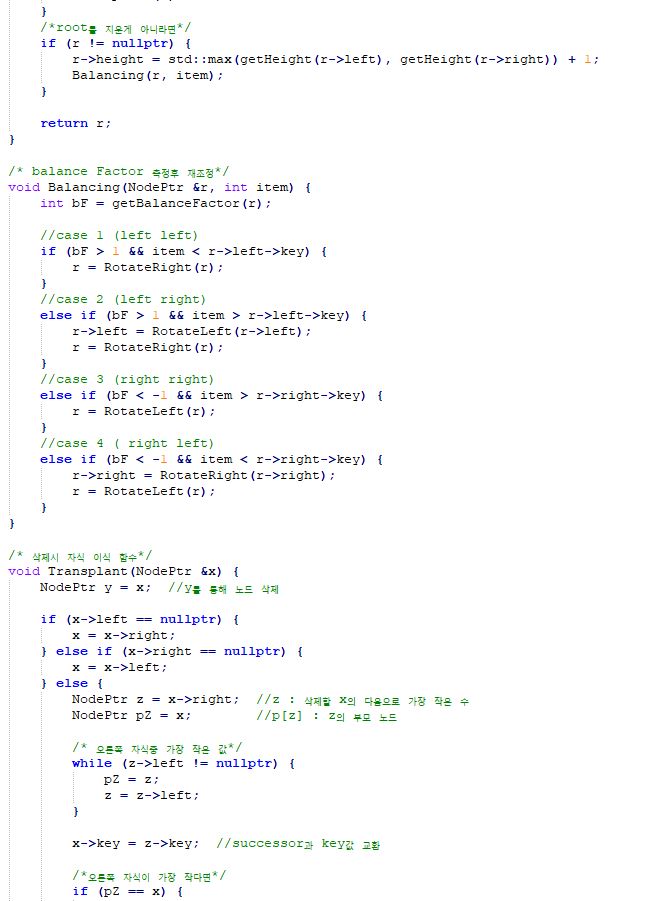
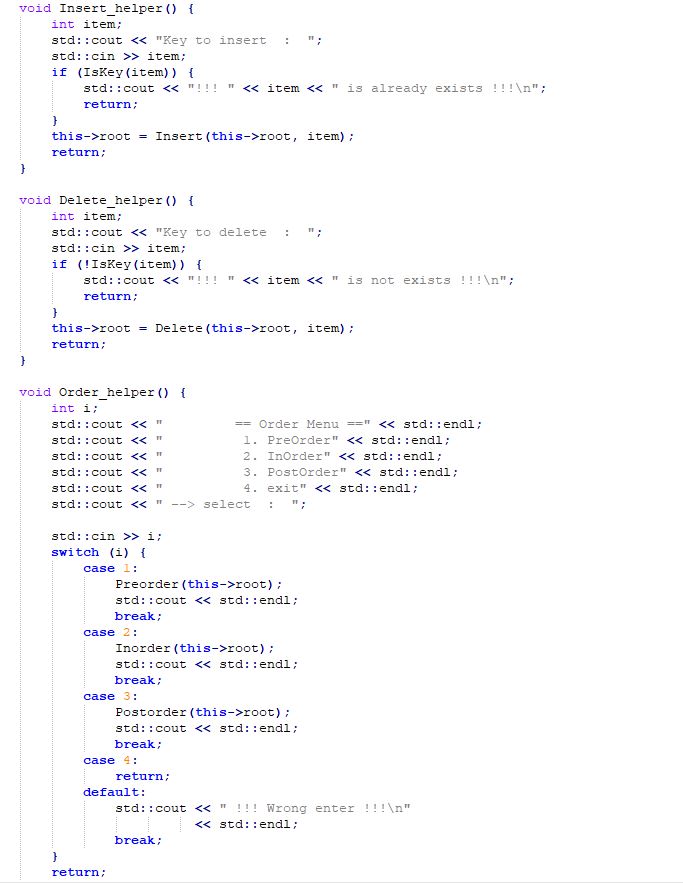
3. Leet code 110번 문제 풀이

문제 원본 링크:
https://leetcode.com/problems/balanced-binary-tree/

문제 설명:
이 문제의 요점을 간단하게 말하면, 해당 트리가 Balanced Binary tree 인지 그냥 Binary Tree 인지 검사하는 문제이다.
검사하려는 해당 트리의 모든 노드들은 Balanced Binary tree 여야 하니까 차례대로 내려가면서 검사하면 된다.
isBalanced()로 해당 노드가 Balanced Binary tree 인지 판별하고, height()에서 노드 깊이 구하고, 이를 비교해서 Left로 보낼지 Right로 보낼지 결정한다.

위 의견들을 종합해서 구현하면 아래 코드와 같다.

1. 이진 탐색 트리(BST)

이진탐색트리에는 아래와 같은 조건을 충족해야한다.
1)모든 노드는 유일한 키를 갖는다.
2)왼쪽 서브 트리 키들은 루트 키보다 작다.
3)오른쪽 서브 트리 키들은 루트 키보다 크다.
4)왼쪽과 오른쪽 서브 트리도 이진탐색트리이다

탐색연산:
트리 구조의 모든 근간이되며, 노드들을 반복해 비교하며 찾는 연산을 거치는 연산이다.

삽입연산:
탐색연산 다음으로 중요하고 실행되는 연산이다. 이유는 이진탐색트리에서는 같은 키 값을 갖는 노드가 없어야하고 또한 탐색에 실패한 위치가 바로 새로운 노드를 삽입하는 위치가 되기 때문이다.

삭제연산:
노드를 삭제하는 것은 이진탐색트리에서 가장 복잡한 연산이다. 노드 삭제 후에도 이진탐색트리의 특성을 반드시 유지해야하기 때문이다. 노드의 삭제는 단말노드삭제, 자식 하나 딸린 노드 삭제, 자식이 두개딸린 노드 식제 케이스로 나뉜다.


3. 문제 풀이
(1) LeetCode #98

루트 노드의 값을 기준으로 노드가 배정되어야 하는데, 왼쪽 오른쪽 서브트리값을 비교하려 하면 예외가 발생할 수 있으므로, 해당노드에 들어갈 수 있는 값의 범위를 전달해야 한다. 1. 해당 노드에 들어갈 수 있는 최소값과 최대값을 설정한다.
2. 매개 변수로 TreeNode* root, TreeNode* low, TreeNode* high를 전달한다.
3. isValid(root->right, root, high)와 isValid(root->left, low, root)를 실행하여 return 값이 false인지 확인한다.

(2) LeetCode #99

1. 두 갈래 검색트리의 두 노드 가 잘못 교환 되었으니, 그 구조를 바꾸지 않고 바르게 돌려놓아야 한다.
2. 아래 보이는 것처럼 inorder 메소드와 recover 메소드를 설정해 교환하고 삭제하는 과정을 거친다.

(3) LeetCode #700

1. node가 null이거나 val을 못찾으면 null값 return한다.
2. 현재 노드의 val이 target val보다 작으면, root의 왼쪽 방향으로 탐색한다.
3. 현재 노드의 val이 target val보다 크면, root의 오른쪽 방향으로 탐색한다.

(4) LeetCode #701

1. 우선순위큐와 힙 내용 정리

우선순위 큐(Priority Queue)란?
먼저 들어온 데이터가 먼저 나가는 선입선출 형태의 자료구조는 큐(Queue)이다.
기본적인 큐 형태에서 데이터 간의 중요도를 따져서, 단순히 선입선출의 형식으로 진행되는 것이 아닌, 중요도를 최우선으로 두어 중요도가 높은 순서대로 데이터를 내보내는 자료구조가 바로 우선순위 큐(Priority Queue)이다.

힙(Heap)이란?
혹시 완전이진트리 구조를 알고있는가? 힙(Heap)은 완전이진트리 중에서도 최대값, 최소값의 데이터를 찾아내고 정렬하는데 가장 유리한 구조이다. 따라서 이런 성질을 가진 힙(Heap)은, 중요도 크기에 따라 데이터를 내보내는 우선순위 큐(Priority Queue)를 표현하기에 가장 알맞은 구조이다.


2. C++를 이용한 우선순위큐 프로그래밍 방법 정리

밑에 나오는 첨부 이미지는 필자가 기능과 구조만 간단히 설명하기 위해 작성한 코드요약본이다.
아래의 코드는 c++를 이용하여 랜덤 숫자 배열을 만들고, 이를 우선순위 큐의 방식을 이용해 큰 숫자 순서로 내보내며 재배열하는 코드를 요약한 것이다. 기본적인 다른 특별한 메소드 없이, 우선순위 큐를 구현하면 대부분 이런 구조이다.

또한, 앞서 일일히 우선순위 큐 클래스를 구현할 필요없이 #Include <queue>를 삽입해 큐 메소드를 사용하면
정말 간단하게 우선순위 큐를 프로그래밍 할 수 있다.

우선순위 큐 메소드를 활용한 힙의 구현을 간단한 코드로 정리 하면 아래와 같다.

3. 백준 1966번 - (프린터 큐) 문제 풀이

문제설명

1. 큐에서 중요도를 확인하여, 중요도가 더 큰 문서가 뒷순서에 존재하면 맨앞에 있는 문서 pop한뒤 맨뒤로 push 한다.

2. 맨앞에있는 문서가 중요도가 가장 높다면 pop하여 출력한다.

입력

맨첫줄-> 총 케이스 개수
두줄묶음씩 한 케이스 ->
첫줄: 문서의 개수, 출력순서 궁금한 현재 문서의 순서
둘째줄: 문서의 중요도 나열

출력
케이스의 첫줄 두번째 정보에 나타나 있는 문서가 몇 번쨰로 인쇄되는지 출력.

풀이
지정한 문서가 언제 출력되는지 알고 싶기에, 문서의 중요도와 인덱스를 둘다 가지고 있어야 문서가 계속 이동해도 찾을 수 있을 것이다.
그래서 큐는 총 2개가 필요한데, 인덱스와 값을 가지고 있는 Queue하나(페어큐라고 하겠습니다.)와 숫자가 내림차순으로 정렬되어 있는 Queue가 하나 필요하다. 굳이 큐를 정렬할 필요 없이, 우선순위 큐를 사용하여 값을 정렬된 값으로 만들게 한다.

코드는 다음과 같다.

  최근 친구가 생전 처음 들어보는 업사이클링 가방 브랜드를 소개해 주었다. 놀랍게도, 그 후 이틀 내내 그 가방을 메고 다니는 사람을 족히 10명은 보았다. 새삼 놀라웠다. 새로운 정보는 늘 내 시야에 크고 작은 영향을 주었고, 그 영향이 크든 작든 아주 미세하게라도 나의 시야를 넓혀주었다. 이렇게 친구로부터 얻게된 사소한 정보도 나의 시야를 넓혀주는데, 하물며 제대로된 정보를 학습할 수 있는 '교육'의 위력은 대체 얼마나 강력할까?라는 생각이 들었다. 대부분의 사람들은 '교육'을 받으면서 자란다. 나는 교육을 받으면 받을수록, 교육의 힘을 조금씩 께닫게 되었다. 교육을 받은 사람과 교육의 받지 못한 사람의 차이는 사실 크다고 생각한다.

  우리는 지난 코로나19 상황에서 큰 교육의 부재를 겪었다고 생각한다. 이러한 학습 손실은 실재로 많은 나라에서 발견되고 있고, 이는 해결해야할 큰 문제이다. 실제로 펜데믹 상황 이후, 중저소득 국가의 정부 중 약 65%와 중상위소득 국가의 35%는 팬데믹이 시작된 이후 교육에 대한 자금 지원을 줄였다. 코로나 19로 인해 전 세계 1억100만 명의 어린이(초등 및 중등학생의 약 9%)가 최소 읽기 능력 한계 이하로 떨어지게 되어 2020년에는 전체 학생 수가 5억8400만 명으로 증가할 것으로 예상된다고 한다. 특히, 가난하거나 취약한 어린이들 사이에서 학교 이수에서의 큰 격차는 더 심해질 가능성이 있으며 , 전염병 확산으로 인한 비대면 원격 학습으로의 전환은 가장 가난한 가정의 어린이들과 다른 취약계층들을 만든다. 상대적으로 가난한 집단은 원격수업에 참여할 준비가 덜 되어 있고, 중퇴할 가능성이 더 높다.

  유아 교육 부분도 상황은 마찬가지다. 대부분의 국가에서 보육 및 조기 교육 시설이 문을 닫았기 때문에 현재 많은 어린 아이들은 전적으로 부모나 다른 보로자에게 의존하고 있다. 집에서. 안전하지 않은 조건, 보호자와의 부정적인 상호작용, 그리고 초기 몇 년 동안 적절한 자극과 학습 기회의 부족은 아이들의 일생 동안 성공의 기회를 감소시킬 수 있다. 유아,청소년기의 교육은 탄력적이고 적응력이 있는 노동자를 창출하는것과 이어진다. 이를 위해 지속적인 교육 및 훈련에 대한 더 광범위한 참여가 필요하다. 기본적인 교육은 먹고사는 문제와 연결되기도 하기 때문에, 지속적인 교육은 생활 개선을 위한 핵심이다.

  이러한 교육의 감소를 회복하기 위해서 우리는 무엇을 해야할까? 일단, 교육환경이 잘 마련 되어야 할것이다. 2016년부터 2019년까지의 데이터에 따르면 전 세계적으로 초등학교 중 1곳 이상이 기본적인 식수나 단일 성별 화장실에 대한 접근성이 부족했고, 3분의 1 이상이 기본적인 손 씻기 시설이 부족했으며, 4명 중 1명은 전기가 공급되지 않았다. 이런 기본적인 공급도 부족하지만, 부가적인 교육 시설, 즉 학교의 인터넷 서비스와 컴퓨터는 훨씬 더 부족하다. 앞서 언급한 부족한 환경들은 전염병 사태와도 큰 관련이 있다. 전염병으로부터 학교에서 아이들을 안전하게 유지하는 데 있어 적절한 위생 시설의 중요성이 강조 되고 있고, 원격 학습을 지원하기 위한 ICT 인프라의 필요성 역시 강조 되고 있지만, 전 세계의 수많은 교육시설들이 그에 반하는 환경임을 짐작할 수 있다. 덧붙여, 적절한 교실 공간, 환기 시설, 그리고 집에서 인터넷과 컴퓨터에 대한 접근과 같은 추가적인 기반 시설 역시 같이 고려되어야 할 문제 인것 같다.

  교육은 살아가는데 절대적으로 필요하다. 가령, 한 사람이 평생 받은 최고의 교육이 고등교육이 아닐지언정, 분명히 그 교육은 그 사람에게 있어 더 넓은 가치를 제공할 것이다. 이는 이제껏 사람이 만들어온 수많은 눈부신 역사,학문,기술들이 증명해 왔다고 생각한다. 나는 교육의 가치는 정말 별 것 아닌 정보 제공에서도 창출 될 수 있다고 믿는다. 내가 지금 작성하는 짧은 글에서도 누군가는 느끼는 바가 있길, 시야가 조금이라도 확장될 수 있길 바라며 첫글을 작성해본다.